HIDROGRAMAS UNITARIOS
130.Un sistema tiene una
función respuesta de pulso discreto con ordenadas 0.1, 0.5, 0.3 y 0.1
unidades. Calcule la salida de este sistema
si tiene un pulso de entrada de: a) 3 unidades, b) 4 unidades, c) 3 unidades en
el primer intervalo de tiempo seguidas por 4 unidades en el segundo.
131.Un sistema tiene la
siguiente función respuesta de pulso unitario. 0.27, 0.36, 0.18, 0.09, 0.05, 0.03,
0.01, 0.01. calcule la salida de este
sistema si tienen una entrada de: a) 2 unidades, b) 3 unidades, c) 2 unidades
en el primer intervalo de tiempo seguidas por 3 unidades en el segundo
intervalo de tiempo.
132.Calcule y grafique la función impulso respuesta u(t), la
función respuesta de paso g(t), la función de respuesta de pulso continuo h(t)
y la función de respuesta de pulso discreto Un para un embalse
lineal con k = 1 h y ![]() .
.
133.Una cuenca se modela
como un embalse lineal con k = 1 h.
Calcule su función de impulso respuesta y su función de respuesta por pulso para pulsos unitarios
de duración de 0.5, 1.0, 1.5 y 2.0 h. Grafique las funciones de respuesta para
0<t<6h.
134.Una cuenca modelada como
un embalse lineal con k = 3 h recibir 75 mm de exceso de lluvia en las primeras
2 horas de una tormenta y 50 mm de exceso de lluvia en las siguientes 2
horas. Calcule el hidrograma de
escorrentía directa parra esta cuenca.
135.Demuestre que el tiempo
de retardo tL entre los centroides del hietograma de exceso de
lluvia y el hietograma de escorrentía directa es igual a la constante de
almacenamiento k para una cuenca modelada como un embalse lineal.
136.El exceso de lluvia y la
escorrentía directa registrados para una tormenta son los siguientes.
|
Tiempo
(h) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Exceso
de lluvia (mm) |
25 |
50 |
|
25 |
|
|
|
|
|
|
Escorrentía
directa (mcub/s) |
0.28 |
3.4 |
11.3 |
15.9 |
14.1 |
12.7 |
7.1 |
2.8 |
1.4 |
Calcule el
hidrograma unitario en una hora.
137.¿Cuál es el área de la
cuenca del problema 136?
138.Deduzca por
deconvolución el hidrograma unitario de
seis horas para la siguiente información de una cuenca con un área de drenaje
de 216 km2, suponiendo una tasa de abstracción de lluvia constante y
un flujo base constante de 20 m3/s.
|
Periodo de seis horas |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Lluvia
(cm) |
1.5 |
3.5 |
2.5 |
1.5 |
|
|
|
|
|
|
|
|
Caudal
(m3/s) |
26 |
71 |
174 |
226 |
173 |
99 |
49 |
33 |
26 |
22 |
21 |
139.A continuación se
presenta el hidrograma de caudales para una tormenta en un área de drenaje
de2.5 mi2.
|
Hora |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Caudal
(cfs) |
52 |
48 |
44 |
203 |
816 |
1.122 |
1.138 |
|
Hora |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
Caudal
(cfs) |
685 |
327 |
158 |
65 |
47 |
34 |
|
Un exceso de lluvia con
intensidad casi uniforme ocurre en forma continua durante las horas 4, 5 y
6. La separación del flujo base se lleva
a cabo graficando el logaritmo del caudal contra el tiempo. Durante el inicio del a creciente, el
logaritmo de flujo base sigue una línea recta con una pendiente determinada del
caudal en las horas 1 a 3. Desde el
punto de inflexión del brazo de recesión del hidrograma de caudal (hora 8), el
logaritmo del lujo base sigue una línea recta con pendiente determinada por el
caudal en las horas 11 a 13. Entre el
pico del hidrograma de caudal y el punto
de inflexión, el logaritmo del flujo base se supone que varía
linealmente. Deduzca el hidrograma
unitario de 1 hora por deconvolución. Transforme las unidades al sistema SI.
140.Una tormenta intensa con
una intensidad aproximadamente constante y duración de seis horas sobre una
cuenca de área de 785 km2 produjo los siguientes caudales Q en m3/s.
|
Hora |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
Q |
18 |
21 |
28 |
44 |
70 |
118 |
228 |
342 |
413 |
393 |
334 |
|
Qb |
18 |
20 |
25 |
32 |
40 |
47 |
54 |
61 |
68 |
75 |
79 |
|
Hora |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
40 |
|
|
Q |
270 |
216 |
171 |
138 |
113 |
97 |
84 |
75 |
66 |
59 |
|
|
Qb |
77 |
73 |
69 |
66 |
63 |
60 |
57 |
55 |
52 |
49 |
|
|
Hora |
42 |
44 |
46 |
48 |
50 |
52 |
54 |
56 |
58 |
60 |
|
|
Q |
54 |
49 |
46 |
42 |
40 |
38 |
36 |
34 |
33 |
33 |
|
|
Qb |
47 |
44 |
42 |
40 |
38 |
37 |
35 |
34 |
33 |
33 |
|
El flujo base Qb
se ha estimado usándola forma del hidrograma observado. Utilice la deconvolución para determinar el
hidrograma unitario de dos horas.
141.Utilice el hidrograma
desarrollado en el problema 120 para calcular el hidrograma de flujo para una
tormenta de 12 horas de duración que tiene 2 cm de exceso de lluvia en las
primeras 6 horas y 3 cm en las siguientes seis horas. Suponga una tasa de flujo base constante de 30 m3/s.
142.Utilice el hidrograma
unitario de una hora desarrollado en el problema 138 para calcular el
hidrograma de caudal para una tormenta de tres horas con una intensidad de
lluvia uniforme de 1,5 pulg/h. Suponga
que las abstracciones son constantes con una tasa de 0,5 pulg/h y que el flujo
base es igual al determinado en el problema 138.
143.Utilice el hidrograma
unitario de dos horas desarrollado en el problema 139 para calcular el
hidrograma de caudal para una tormenta de cuatro horas en la cual cayeron 5 cm
de exceso de lluvia en las primeras dos horas y 6 cm en las siguientes dos
horas. Suponga el mismo flujo base que
se dio en el problema 139.
144.El hidrograma unitario
de seis horas de una cuenca que tiene un área de drenaje igual a 393 km2
es como sigue:
|
Tiempo (h |
0 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
|
Hidrograma unitario (m3/s/cm) |
0 |
1,8 |
30,9 |
85,6 |
41,8 |
14,6 |
5,5 |
1,8 |
Para una tormenta sobre
la cuenca que tiene un exceso de lluvia de 5 cm para las primeras seis hora y 15
cm para las siguientes seis horas, calcule el hidrograma de caudal suponiendo
un flujo base constante de 100 m3/s.
145.El hidrograma unitario
de una hora para una cuenca está dado a continuación. Determine la escorrentía para esta cuenca producida por el patrón
de tormenta dado. Las abstracciones
tienen una tasa constante de 0,3 pulg/h.
¿Cuál es al área de esta cuenca?.
|
Tiempo (h) |
1 |
2 |
3 |
4 |
5 |
6 |
|
Precipitación (pulg) |
0,5 |
1,0 |
1,5 |
0,5 |
|
|
|
Hidrograma unitario (cfs/pulg) |
10 |
100 |
200 |
150 |
100 |
50 |
146.Utilice el mismo
hidrograma del problema 145 y determine el hidrograma de escorrentía directa para
una tormenta de dos horas con 1 pulg de exceso de lluvia para la primera hora y
2 para la segunda hora. ¿Cuál es el área de esta cuenca?.
147.Una cuenca de uso
agrícola se urbanizó en un período de 20 años.
Un hidrograma unitario triangular se desarrolló para esta cuenca para un
exceso de lluvia de duración de una hora.
Antes de la urbanización, la tasa promedio de infiltración y otras
pérdidas era 7.5 mm/h y el hidrograma unitario tenía un caudal pico de 0.44
mcub/s/mm y 4 h y un tiempo base de 9 h.
Después de la urbanización, debido al incremento en superficies
impermeables, la tasa de pérdida bajó a 3.5 mm/h, el caudal pico del hidrograma
unitario se incrementó a 0.66 mcub/s/mm, ocurriendo a 1 h y el tiempo base se
redujo a 6 h. Para una tormenta de dos
horas en el cual cayó 25 mm de lluvia en primera hora y 12 mm en la segunda
hora, determine los hidrogramas de escorrentía directa antes y después de la
urbanización.
148.Las ordenadas a
intervalos de una hora de un hidrograma unitario de una hora son (en cfs/pulg):
269, 538, 807, 645, 484, 323 y 161.
Calcule el hidrograma de escorrentía directa para una tormenta de dos
horas en la cual ocurre un exceso de lluvia de 4 pulg a una tasa
constante. ¿Cuál es el área de la
cuenca (mi-2)?.
149.El hidrograma unitario
triangular de 10 minutos para una cuenca tiene un caudal pico de 100 cfs/pulg
en el minuto 40 y una duración total de 100 min. Calcule el hidrograma de
caudal para esta cuenca para una tormenta en la cual caen 2 pulg de lluvia en
los primeros 10 min y 1 pulg en los segundos 10 minutos, suponiendo que la tasa
de pérdidas es f = 0,6 pulg/h y la tasa de flujo
base es 20 cfs.
150.El 19 y 20 de Julio de 1979,
la tormenta en la cuenca del riachuelo
Shoal en Northwest Park en Austin, Texas, produjo los siguientes valores de
lluvia-escorrentía
|
Tiempo (h) |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
|
Lluvia (pulg) |
1,17 |
0,32 |
0,305 |
0,67 |
0,545 |
0,10 |
0,06 |
|
Escorrentía directa
(cfs) |
11,0 |
372,0 |
440,0 |
506,0 |
2110,0 |
1077,0 |
429,3 |
|
Tiempo (h) |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
7,0 |
|
Escorrentía directa
(cfs) |
226,6 |
119,0 |
64,7 |
39,7 |
28,0 |
21,7 |
16,7 |
|
Tiempo (h) |
7,5 |
8,0 |
8,5 |
9,0 |
|
|
|
|
Escorrentía directa
(cfs) |
13,3 |
9,2 |
9,0 |
7,0 |
|
|
|
Determine el hidrograma
unitario de media hora utilizando programación lineal. Suponga que es válida una tasa uniforme de
pérdidas. El área de la cuenca es 7,03
mi2. Compare el hidrograma unitario con aquel determinado en el
ejemplo 118 para esta cuenca. Transforme a unidades SI.
151.Una tormenta que ocurrió
el 16 de Abril de 1977, en la cuenca del riachuelo Shoal en Northwest Park, Austin,
Texas, produjo los siguientes valores de lluvia-escorrentía:
|
Tiempo (h) |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
|
Lluvia (pulg) |
0,28 |
0,12 |
0,13 |
0,14 |
0,18 |
0,14 |
0,07 |
|
Escorrentía directa
(cfs) |
32 |
67 |
121 |
189 |
279 |
290 |
237 |
|
Tiempo (h) |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
7,0 |
|
Escorrentía directa
(cfs) |
160 |
180 |
72 |
54 |
44 |
33 |
28 |
|
Tiempo (h) |
7,5 |
8,0 |
8,5 |
9,0 |
|
|
|
|
Escorrentía directa
(cfs) |
22 |
20 |
18 |
16 |
|
|
|
Determine el hidrograma
unitario de media hora usando programación lineal. Suponga que es válida una tasa uniforme de pérdidas. El área de la cuenca es 7,03 mi2.
Compare el hidrograma unitario con el desarrollado en el ejemplo 136 para esta
cuenca.
152.Combine la información
de los problemas 132 y 133 y calcule un hidrograma unitario compuesto para esta
cuenca utilizando programación lineal.
Compare el hidrograma unitario compuesto con aquellos determinados para las
tormentas individuales.
153.Resuelva el problema 150
por regresión lineal.
154.Resuelva el problema 151
por regresión lineal.
155.Resuelva el problema 152
por regresión lineal.
156.En la ciudad de Austin,
Texas, se aplican las ecuaciones generalizadas (7.7.9)-(.7.7.13) del libro de
Chow, Maidment y Mays para determinar los parámetros de hidrogramas unitarios
de 10 minutos de duración para cuencas pequeñas. Determine los hidrogramas unitarios de 10 minutos para niveles de
impermeabilidad de 10, 40 y 70 en una cuenca que tiene unárea de 0,42 mi2
con un canal principal de longitud de 5,760 pies. El canal principal tiene una pendiente de 0,015 pie/pie tal como
se definió en la sección 7.7. Suponga f = 0,8. Grafique los tres hidrogramas unitarios en
le misma gráfica.
157.Utilizando las
ecuaciones de hidrograma unitario de 10 minutos (7.7.9.) – (7.7.13) del libro de Chow, Maidment y Mays desarrolle
el hidrograma unitario para un pequeña cuenca de 0,3 mi3 de área que
tiene un canal principal con pendiente de 0,009 pie/pie. El área del canal principal es de 2.000 pies
y el porcentaje de permeabilidad es 25.
Después, desarrolle el hidrograma unitario de 10 minutos para la misma
cuenca suponiendo que la longitud del canal principal es 6.000 pies. Grafique y compare los dos hidrograma
unitarios. Suponga que n = 0,05 para el
canal principal.
158.Determine hidrogramas de
escorrentía directa usando los dos hidrogramas unitarios de 10 minutos
desarrollados en el problema anterior para las cuencas con longitudes de canal
principal de 2.000 pie y de 6.000 pird.
Considere una tormenta que tiene una precipitación de 1.2 pulgadas
distribuida uniformemente sobre los primeros 30 minutos y de 1,5 pulgadas en
los siguientes 30 minutos. Las pérdidas
por infiltración se determinan usando el método SCS descrito en el capítulo 5
para un número de curva CN = 85.
159.El hidrograma unitario
de 10 minutos para una cuenca con 0,86 mi2 tiene ordenadas de 10
minutos en cfs/pulg de 134, 392, 475, 397, 329, 273, 227, 188, 15, 129, 107,
89, 74, 61, 51, 42, 35, 29, 24, 10, 17, 14, 11, ……. Determine el coeficiente de pico Cp para el método de
Snyder. La longitud del canal principal
es 10.500 pies y Lc = 6.000 pies.
Determine el coeficiente Ct.
160.Algunas ecuaciones para
calcular el tiempo de retardo se han reportado en la literatura técnica. Una de estas ecuaciones, que también
considera la pendiente de la cuenca, fue presentada por Linsley, Kohler y
Paulhus (1982):
![]()
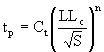
Para una pendiente de
cuenca de S = 0,008 y n = 0,4, determine el coeficiente Ct para el
hidrograma unitario del problema anterior. Compare los resultados usando las expresiones
propuestas por Rodríguez-Benítez y Arteaga- Benítez.
161.Se ha determinado la
siguiente información para una cuenca A y su hidrograma unitario de dos horas:
área = 100 mi2, Lc = 10 mi, L = 24 mi, tpR = 6
h, Qr = 9.750 cfs/pulg, W50 = 4,1 h y W75 = 2
h. La cuenca B, la cueal se supone que
es hidrológicamente similar a la cuenca A, tiene las siguientes
características: área = 70 mi2, L = 15,6 mi y Lc = 9,4
mi. Determine el hidrograma unitario
sintético de una hora para la cuenca B.
144 a)
Determine los coeficientes Cp y Ct para una cuenca
de área 100 mi2 con L = 20
mi y LC = 12 mi para tR = 2 h y tpR = 5
h. El pico del hidrograma unitario es
9,750 cfs/pulg. Suponga que se puede aplicar el hidrograma
unitario sintético de Snyder.
b)
Determine el hidrograma unitario de dos horas para el área más alta de 70 mi-2
de la misma cuenca, la cual tiene L = 12,6 mi y Lc = 7,4 mi. Los valores de W75 y W para el
área total de 100 mi-2 son 2,0 h y 4,2 h, respectivamente.
162.La cuenca del riachuelo
Gimlet en Sparland, Illinois, tiene un área de drenaje de 5,42 mi2;
la longitud del canal principal es 4,45 mi y la longitud de dicho canal desde
la salida de la cuenca a un punto cercano al centro de gravedad de ésta es 2,0
mi. Usando Ct = 2,0 y Cp
= 0-625, determine el hidrograma unitario sintético estándar para esta
cuenca. ¿Cuál es la duración
estándar? Utilice el método de Snyder y
de Rodríguez-Benítez para determinar el hidrograma unitario de 30 minutos para
esta cuenca.
163.La cuenca del riachuelo
Odebolt cerca de Arthur, Ohio tiene un área de 39,3 mi2; la longitud
del canal principal es 18,10 mi y la longitud de dicho canal desde la salida de
la cuenca a un punto cercano al centroide de ésta es 6,0 mi. Usando Ct = 2,0 y Cp =
0,625, determine el hidrograma unitario sintético estándar y el hidrograma
unitario de dos horas para esta cuenca.
164.Una cuenca de 8 mi-2
tiene un tiempo de concentración de 1,0 h.
Calcule el hidrograma unitario de 10 minutos para esta cuenca utilizando
el método del hidrograma unitario triangular SCS. Determine el hidrograma de escorrentía directa para una tormenta de 20 minutos con 0,6 pulg de
exceso de precipitación en los primeros 10 minutos y 0,4 pulg en los segundos
10 minutos.
165.Un hidrograma unitario
sintético triangular se desarrolló utilizando el método de Soil Conservation
Service, tiene qp = 2,900 cfs/pulg, Tp = 50 min y tr
= 10 min. Calcule el hidrograma de
escorrentía directa para una tormenta de 20 minutos con 0,66 pulg de lluvia en
los primeros 10 minutos y 1,70 pulg en los siguientes 10 minutos. La tasa de pérdida de lluvia es f = 0,6 pulg/h a lo largo
de la tormenta.
166.Para la información dada
en el problema 139 utilice la suposición
de una intensidad constante de lluvia en las horas 4 a 6 para construir
el hidrograma S. Utilice el hidrograma
S para calcular los hidrogramas unitarios de una, tres y seis horas.
167.Para la información dada
en el problema 139 la suposición de una intensidad de lluvia constante para las
6 horas para construir el hidrograma S de esta cuenca. Con base en el hidrograma S, determine los
hidrogramas unitarios de 2, 6 y 12 horas para esta cuenca.
168.Las ordenadas de un
hidrograma unitario de una hora especificadas en intervalos de una hora son (en
cfs/pulg): 45, 60, 22, 8 y 1. Calcule
el área de la cuenca, el hidrograma S y el hidrograma unitario de dos horas para esta cuenca.
169.Empleando el hidrograma
unitario (1 cm) de 4 horas de duración que se presenta en la tabla siguiente,
determinar el caudal máximo que resulta de 3 períodos consecutivos de
lluvia de 4 horas de duración iguales a
9 mm, 35 mm y 22 mm respectivamente.
El área de la cuenca es
24,6 Km2.
|
Hora |
Caudal (m3/s) |
Hora |
Caudal (m3/s) |
|
0 |
0 |
8 |
6,1 |
|
1 |
0,5 |
9 |
4,7 |
|
2 |
1,6 |
10 |
3,5 |
|
3 |
4,9 |
11 |
2,5 |
|
4 |
9,5 |
12 |
1,7 |
|
5 |
12,5 |
13 |
1,0 |
|
6 |
11,3 |
14 |
0,5 |
|
7 |
8,1 |
15 |
0 |
Desprecie el
escurrimiento subterráneo.
170.Los datos siguientes
resumen el caudal y lluvia observados
en una tormenta aislada en la cuenca del Arroyo San Francisquito en
California. La cuenca tiene un área de 56 Km2.
a) Derivar el hidrograma
unitario
b) Calcular la curva S
para el hidrograma anterior
c) Calcular el
hidrograma unitario de 6 horas
d) Estimar el caudal
máximo superficial proveniente de dos períodos de lluvia efectiva de 6 horas
iguales a10 mm y 32 mm respectivamente.
|
Fecha |
hora |
caudal m3/s |
Lluvia mm |
Fecha |
Hora |
Caudal m3/s |
Lluvia mm |
|
Mar 4, 1951 |
10 |
0,7 |
0 |
Mar 5 |
12 |
13,6 |
|
|
|
12 |
0,9 |
0 |
|
14 |
11,5 |
|
|
|
14 |
2,2 |
13 |
|
16 |
10,1 |
|
|
|
16 |
11,8 |
13 |
|
18 |
8,9 |
|
|
|
18 |
21,5 |
8 |
|
20 |
8,0 |
|
|
|
20 |
29,2 |
8 |
|
22 |
7,4 |
|
|
|
22 |
31,7 |
8 |
|
24 |
6,7 |
|
|
|
24 |
29,2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mar 5, |
2 |
27,5 |
0 |
Mar 6 |
2 |
6,4 |
|
|
|
4 |
24,6 |
0 |
|
4 |
6,0 |
|
|
|
6 |
21,9 |
|
|
6 |
5,7 |
|
|
|
8 |
18,4 |
|
|
8 |
5,5 |
|
|
|
10 |
15,7 |
|
|
10 |
5,3 |
|
|
|
|
|
|
|
12 |
5,0 |
|
171.La tabla siguiente
presenta el escurrimiento superficial proveniente de una tormenta de 3 horas de
duración sobre una cuenca de 312 Km2. Derive el hidrograma unitario
(I cm) de 12 horas de duración.
|
Caudal en m3/s |
|||
|
Hora |
Día 1 |
Día 2 |
Día 3 |
|
3 |
0 |
82 |
24 |
|
6 |
0 |
70 |
20 |
|
9 |
108 |
60 |
16 |
|
12 |
180 |
62 |
12 |
|
15 |
150 |
44 |
8 |
|
18 |
130 |
38 |
6 |
|
21 |
112 |
32 |
4 |
|
24 |
108 |
28 |
0 |