PRECIPITACION
1. Calcule la velocidad
terminal de una gota de lluvia de 0.8 mm a presión atmosférica estándar y temperatura de aire de 20ºC si la masa específica del aire es 1.20 kg/m3.
2. Una corriente de aire que
se mueve verticalmente hacia arriba a 5 m/s, contiene gotas de lluvias de
varios tamaños. Calcule la velocidad de
un gota de 2 mm de diámetro y determine
si está subiendo o cayendo. Repita este
ejercicio para una gota de 0.2 mm de diámetro.
Suponga presión atmosférica estándar, temperatura de aire de 20ºC y masa
específica del aire de 1.20 kg/m3.
3. Si una gota de lluvia
esférica de diámetro D, masa específica 
y coeficiente de
arrastre Cd, se suelta desde el reposo en una atmósfera de masa
específica 
, demuestre que la distancia z que se necesita para alcanzar
una velocidad V está dada por
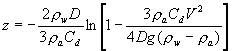
Suponga V 
velocidad terminal
4. Utilizando la ecuación
anterior, calcule la distancia que una gota de 0.8 mm necesitaría caer para
alcanzar el 50, el 90 y el 99% de su velocidad terminal a presión atmosférica
estándar y 20ºC par ala temperatura del aire.
5. Gotas de lluvia de 1 mm
de diámetro caen sobre un suelo erosionable.
Calcule la energía de impacto de cada gota. Suponga condiciones
atmosféricas estándar de 20ºC de
temperatura y 101.3 kPa de presión de aire.
Tenga en cuenta que la gota perderá toda su energía cinética en el
impacto.
6. Resuelva el problema
anterior para gotas de 0.1, 0.5, 1 y 5
mm de diámetro y construya un gráfico mostrando la variación de energía de
impacto en función del tamaño de la gota.
7. Demuestre que la
proporción en humedad entrante que se precipita para el modelo de celda de
tormentas eléctricas, está dada por (qv1-qv2)/qv1(1-qv2),
donde qv1 y qv2 son
la humedades específicas de las corrientes de aire de entrada y salida
respectivamente.
8. Resuelva el problema
3.3.2 (Chow, Maidment y Mays) para
determinar la intensidad de precipitación se la temperatura superficial es de
20ºC. ¿Cuál es el porcentaje de reducción en la intensidad de precipitación si
la temperatura superficial baja de 30 a 20ºC?
Calcule el tasa de liberación de calor latente en la tormenta a través
de la condensación de vapor de agua para producir la precipitación.
9. Resuelva el ejemplo
3.3.2 (Chow, Maidment y Mays) para
determinar la precipitación de una tormenta si la salida de humedad se localiza
a una elevación de 5 km. ¿Qué porcentaje de la humedad entrante se precipita
ahora?
10. Coloque un pedazo de
papel calcante sobre el mapa de isoyetas para la tormenta de Johnstown (véase
la figura 3.4.1ª) y trace la isoyetas
de precipitación dentro del área limitada por la isoyeta de 2 pulg.
11. Calcule la profundidad
promedio de precipitación sobre el área de 10 mi x 10 mi que se muestra para la
tormenta de Austin (véase la figura 3.41b libro de Chow, Maidment y Mays).
12. La siguiente información
de lluvia se registró en el pluviómetro 1-Bol para la tormenta del 24 al 25 de
mayo de 1981 en Austin, Texas:
|
Tiempo (min) |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
Lluvia (mm) |
0 |
1.8 |
5 |
6.4 |
5.6 |
5.5 |
4.1 |
3.9 |
0.8 |
Represente gráficamente
el hietograma de lluvia. Calcule y
dibuje el hietograma de lluvia acumulada.
Determine la máxima profundidad e intensidad registrada en 10, 20 y 30
minutos para esta tormenta. Compare la
intensidad de 30 minutos con valores usuales en Santiago.
13. La siguiente información
de lluvia incremental se registró gráficamente en el hietograma del 24 de mayo
de 1981. Represente graficamente el
hietograma de lluvia. Calcule y dibuje
el hietograma de la lluvia. Determine
la profundidad máxima y la intensidad de lluvia para 5, 10, 30, 60, 90 y 120
minutos para esta tormenta.
|
Tiempo (min) |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
Lluvia (mm) |
0 |
2.3 |
0.00 |
0.8 |
3.3 |
2.5 |
3.3 |
5.3 |
9.4 |
3.2 |
7.8 |
|
Tiempo (min) |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
105 |
|
Lluvia (mm) |
12.7 |
2.5 |
3.3 |
3.5 |
3.1 |
4.1 |
3.8 |
4.6 |
0.8 |
12.5 |
10.2 |
|
Tiempo (min) |
110 |
115 |
120 |
125 |
130 |
135 |
140 |
145 |
150 |
|
|
|
Lluvia ( mm) |
9.9 |
6.6 |
10.4 |
10.8 |
11.5 |
4.3 |
4.4 |
4.1 |
2.5 |
|
|
14. La forma de una cuenca
de drenaje puede aproximarse por un polígono cuyos vértices se localizan en las
siguientes coordenadas: (5, 5), (-5,
5), (0,-10) y se tienen pluviómetros localizados dentro y cerca de la cuenca tal como sigue:
|
Número del pluviómetro |
Coordenadas |
15. Lluvia registrada (mm) |
|
1 |
(7, 4) |
62 |
|
2 |
(3, 4) |
59 |
|
3 |
(-2, 5) |
41 |
|
4 |
(-10, 1) |
39 |
|
5 |
(-3, -3) |
105 |
|
6 |
(-7, -7) |
98 |
|
7 |
(2, - 3) |
60 |
|
8 |
(2, -10) |
41 |
|
9 |
(0, 0) |
81 |
Todas las coordenadas se
expresan en kilómetros. Determine la
lluvia promedio en la cuenca
utilizando: a) el método de la media
aritmética; b) el método de Thiessen, y c) el método de las isoyetas. Para el método de Thiessen empiece dibujando
un polígono alrededor del pluviómetro 9, luego dibuje los polígonos alrededor
de los pluviómetros 2, 3, 5 y 7; para
el método de las isoyetas, dibújelas con lluvia máxima a lo largo de una línea
desde el suroeste hacia el noreste a través de (-3, -3).
.
23. Cuatro pluviometros que
se localizan dentro de un área rectangular con sus cuatro esquinas en (0, 0),
(14, 13) y (14, 0), tienen las siguientes coordenadas y registros de lluvia:
|
Localización
del pluviómetro |
Lluvia
(mm) |
|
(2, 9) |
15 |
|
(7, 11) |
20 |
|
(12, 10) |
25 |
|
(6, 2) |
43 |
Todas las coordenadas se expresan
en kilómetros. Calcule la lluvia
promedio en el área utilizando el método de Thiessen.